幾何学的図形に色を塗ることで、子供たちは色の知覚を改善し、形の違いに注意を払い、創造性を発達させ、リラックスさせることができます。それぞれの絵はユニークで個性的であるため、数字を着色することはあなた自身とあなたの個性を表現する素晴らしい方法です.幾何学的図形は、長方形、円、三角形など、空間内のオブジェクトの幾何学的関係を表す形状またはパターンです。着色のためのフォーム。


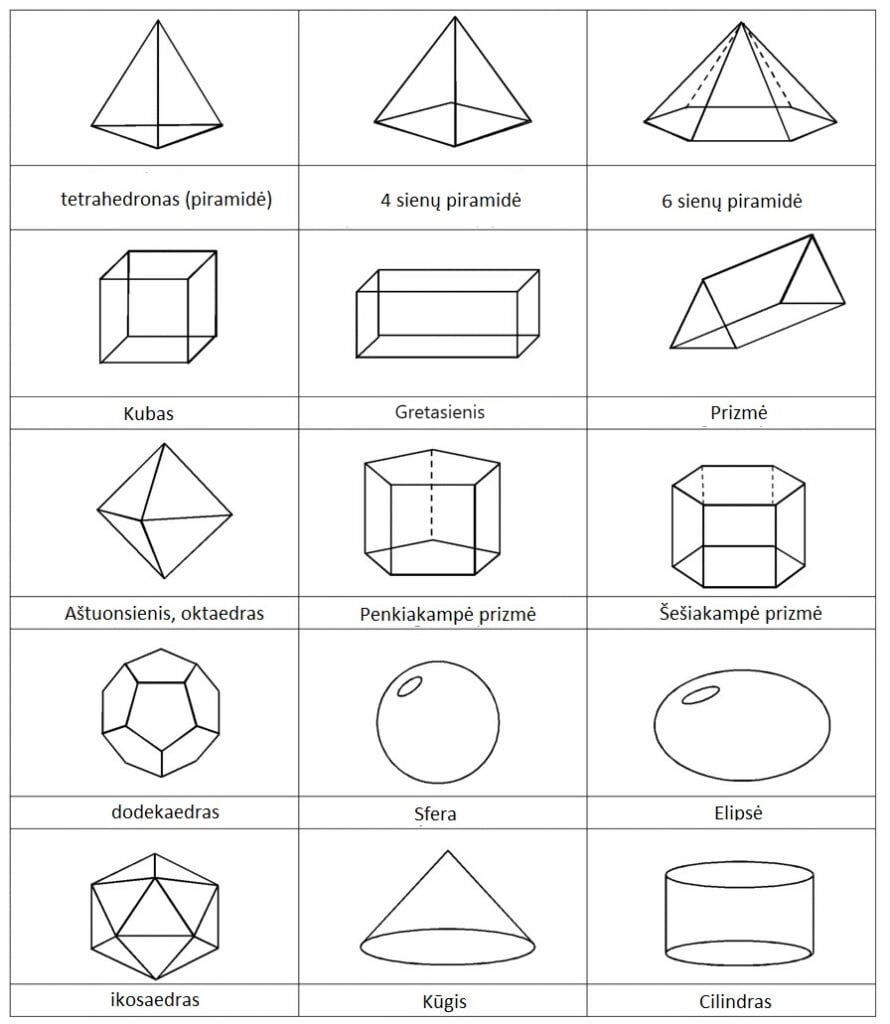
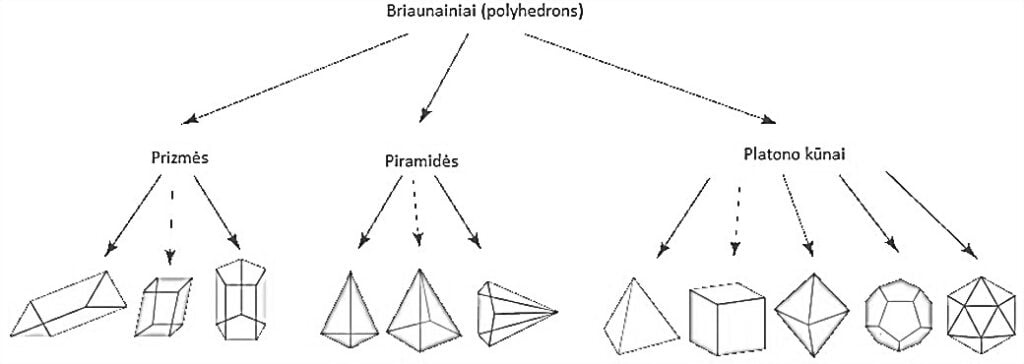






着色のための写真

幾何学的図形に色を塗ることで、子供たちは色の知覚を改善し、形の違いに注意を払い、創造性を発達させ、リラックスさせることができます。それぞれの絵はユニークで個性的であるため、数字を着色することはあなた自身とあなたの個性を表現する素晴らしい方法です.幾何学的図形は、長方形、円、三角形など、空間内のオブジェクトの幾何学的関係を表す形状またはパターンです。着色のためのフォーム。
































